前言

当前有跟着老师做一些深度学习的研究，在研究的过程中我意识到了深度学习基础知识的重要性。所以回来把花书好好的啃一遍。这篇文章是这个系列的第一篇，希望我能够坚持把这本书给啃完吧😊。

在机器学习领域经常需要进行大量的数值计算，常见的操作有优化（optimization，找到一个任务达到最大值/最小值时的参数）和线性方程的解决系统。当一个方程中包含着大到内存都装不下的实数时，即使只是评估一个数学方程对于电子计算机而言也是非常困难的。使用计算机的有限来毕竟一些无限的数，这个本身就是矛盾的。花书中本章主要就是解决这样的问题

上溢和下溢

在数字计算机中一个最基本的问题就是我们需要在有限的数字系统中去表示无限多个实数。这意味着当我们在使用计算书表示数字的时候几乎所有的实数都会产生一个近似误差。很多情况下这个误差都是可以忽略的。书中叫他rounding error，可以很直观的感觉出来就是误差中的“边缘人士”。但是rounding error在多个操作中如果积累的过多也会造成实验的失败。

rounding error的一种经典的形式就是下溢 $underflow$ 。下溢发生在数字接近0的时候。举一个例子，我们经常会避免除数为0的情况（在一些硬件环境下会报错，有的环境会返回一个not-a-number的值）同样的我们也会避免对0求对数。

另一种形式的rounding error叫做上溢 $overflow$ . 上溢发生在一个数字非常的大的时候（接近正无穷和负无穷）。上溢和下溢都是rounding error,是我们在进行数值计算的时候应该尽量避免的。在训练的过程中我们也知道loss是nan肯定不是啥好事。

一个必须对抗上溢和下溢情况的函数就是softmax函数了，softmax函数的定义如下：

$softmax(x)_i = \frac{exp(x_i)}{\sum_{j=1}^nexp(x_j)}$

上溢和下溢会对softmax函数产生比较大的影响。假设所有的 $x_i$ 。

代码实现：

import numpy as np
import numpy.linalg as la
x = np.array([1e7,1e8,2e5,2e7])
y = np.exp(x)/sum(np.exp(x))
print('上溢：',y)
x = x-np.max(x) # 减去最大值
y = np.exp(x)/sum(np.exp(x))
print("上溢处理：",y)

1 2	上溢： [nan nan nan nan] 上溢处理： [0. 1. 0. 0.]

这样就行优化之后其实还有一个问题就是如果输入的全部都是0的话还是会产生下溢的问题。这意味着如果我们在这个情况下将softmax计算的结果在传入一个log函数中时我们将会得到负无穷这一个错误的结果。当然了我们也可以使用让softmax稳定的方法来让log函数稳定。

x = np.array([-1e10,-1e9,-2e10,-1e10])
y = np.exp(x) / sum(np.exp(x))
print("下溢：",y)
x = x-np.max(x)
y = np.exp(x)/sum(np.exp(x))
print("下溢处理：",y)
print("log softmax(x):",np.log(y))

# 对log softmax 函数进行下溢处理
y = x - np.log(sum(np.exp(x)))
print("logsoftmax(x):", y)

下溢： [nan nan nan nan]
下溢处理： [0. 1. 0. 0.]
log softmax(x): [-inf   0. -inf -inf]
logsoftmax(x): [-9.0e+09  0.0e+00 -1.9e+10 -9.0e+09]

花书中写了，一个好的框架的底层库应该都已经帮你尽可能的解决了这些问题。如果你不是一个底层框架的开发人员那么你大可以调用别人写好的库。但是如果你是一个框架底层的开发人员那么你就要把这些数字计算的问题印在心中。

Poor Conditioning

Conditioning 表示一个函数对于细小的输入变化有多快。对于科学计算来说一个函数如果输入有轻微的变化，函数结果也跟着有非常大的变化将会成为一个非常大的问题。因为输入中的rounding error在输出时会变的非常巨大。

举一个例子，一个函数 $f(x)=A^{-1}x$ )为:

$\max _{i, j}\left|\frac{\lambda_{i}}{\lambda_{j}}\right|$

这个比例就是最大的特征值与最小特征值之间的比例。当这个值较大的时候，矩阵的逆就会对输入误差敏感。这种敏感是矩阵本身的特性，而不是因为求逆取整误差带来的。

这一点也是比较底层的计算特性，花书的作者也自己用C和CUDA去写过深度计算框架darknet，所以他在介绍的时候会介绍一些偏底层的内容。我们如果使用成熟的框架的话就可以少考虑这一类的问题。

基于梯度的优化器

大多数的深度学习算法都要用到优化器( $optimiztion$ 达到最大值或者最小值。

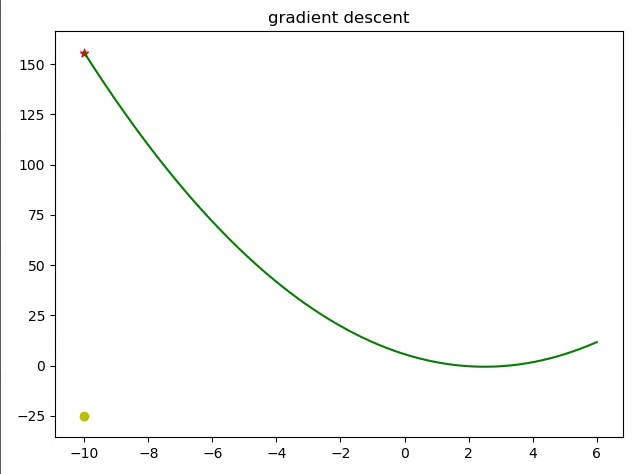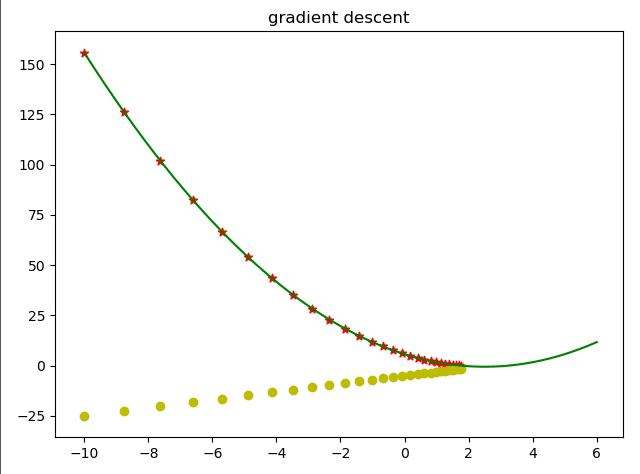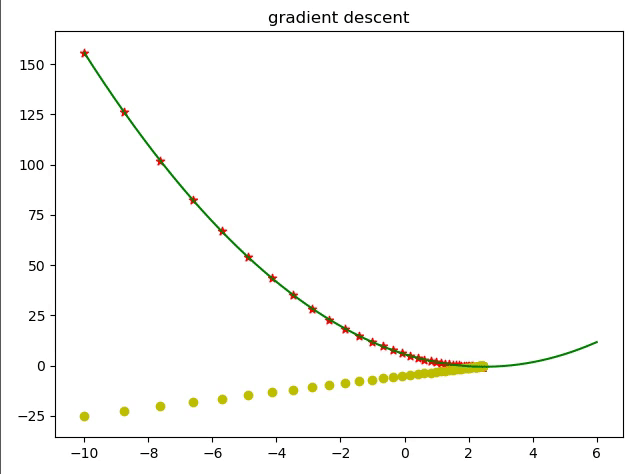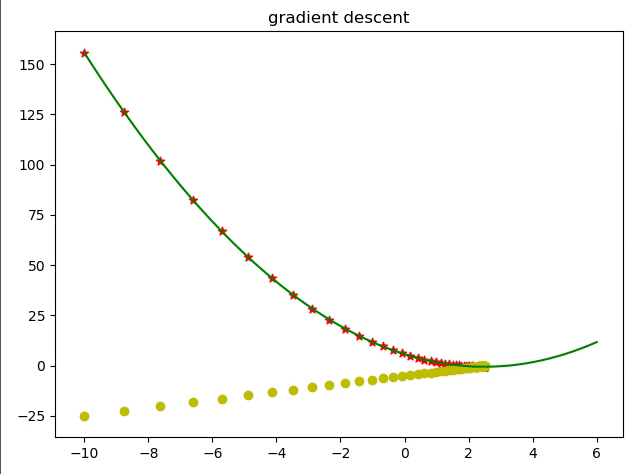
简单的来说优化器就是通过求导的方式让函数的值达到最大值或者最小值。 导数经常被用来求一个函数的最值，因为它告诉了我们怎样去改变x来优化 $y$ 这是因为我们在进行梯度更新的时候都是一小步一小步的会通过学习率来限制学习速度。

当导数等于0的时候，求导就不能给我们的更新方向提供信息了。导数等于0的点叫做stationary points。当一个地方导数等于0但是有其他的点数值比该点小的话，这个点就叫做局部极小点。花书中还对鞍点等梯度下降容易出现的问题进行了描述，这里就不再赘述了。

总结一下就是：梯度下降法（Gradient Descent）的目标函数是最小化具有多维的输入： $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$ 。梯度下降法建议的新的点为：
$\boldsymbol{x}^{\prime}=\boldsymbol{x}-\epsilon \nabla_{\boldsymbol{x}} f(\boldsymbol{x})$
现在我们使用代码来用梯度下降算法实现求解一个函数的解。

[例子] 首先引入线性最小二乘公式：
$f(\boldsymbol{x})=\frac{1}{2}\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b}\|_{2}^{2}$
建设我们希望找到最小化该式的 $x$ 值。

可以计算梯度得到：

$\nabla_{\boldsymbol{x}} f(\boldsymbol{x})=\boldsymbol{A}^{\top}(\boldsymbol{A} \boldsymbol{x}-\boldsymbol{b})=\boldsymbol{A}^{\top} \boldsymbol{A} \boldsymbol{x}-\boldsymbol{A}^{\top} \boldsymbol{b}$

那么我们就根据梯度下降算法来求解该式最小时的 $x$ 值。

import numpy as np
# 初始化参数
x0 = np.array([1.0,1.0,1.0])
A = np.array([[1.0,-2.0,1.0],[0.0,2.0,-8.0],[-4.0,5.0,9.0]])
b = np.array([0.0,8.0,-9.0])
epsilon = 0.001 # 学习率
delta = 1e-3 # 允许的误差值
# 这里正确的解为： [29, 16, 3]

def matmul_chain(*args):
  """
  矩阵相乘
  """
  if len(args) == 0: 
    return np.nan 
  result = args[0]
  for x in args[1:]:
    result = result@x 
  return result

def gradient_decent(x, A, b, epsilon, delta):
  # 当梯度更新不动的时候就停止
  while la.norm(matmul_chain(A.T, A, x)-matmul_chain(A.T, b)) > delta:
    # 梯度更新
    x -= epsilon*(matmul_chain(A.T, A, x)-matmul_chain(A.T, b)) 
  return x

gradient_decent(x0, A, b, epsilon, delta)
# out: array([27.82277014, 15.34731055,  2.83848939])