「信息安全数学基础」二次同余式与平方剩余

平方剩余(二次剩余)

（a，m）= 1，$x^2\equiv \ a\ mod\ m$有解，则a叫模m的平方剩余；P125

欧拉判别定理

如何快速的判断某个数是否是模p的平方剩余；

$x^2\equiv\ a\ mod\ p$，（等价）则a是模p的平方非剩余 P129

Legendre（勒让德）

用于帮忙判断同余式是否有解

对于同余式：$x^2 \equiv a(mod \ p)$;
$\left(\frac{a}{p}\right)=\begin{cases}1,&\text{若a是模p的平方剩余}\\-1,&{若a是模p的平方非剩余}\\0,&\text{若p|a}\end{cases}$
如果p是奇素数，那么还有如下的性质：

$\left(\frac{1}{p}\right)=1$

$\left(\frac{-1}{p}\right)=(-1)^{\frac{p-1}{2}}$

$\left(\frac{2}{p}\right)=(-1)^{\frac{p^2-1}{8}}$

一些运算性质：

( i ) $\left(\frac{a+p}{p}\right) = \left(\frac{a}{p}\right)$ 周期性

( ii ) $\left(\frac{a \cdot b}{p}\right) = \left(\frac{a}{p}\right)\left(\frac{b}{p}\right)$

勒让德符号的性质：

• 周期性：$\left(\frac{a+p}{p}\right)=\left(\frac{a}{p}\right)$
• 完全可乘性：$\left(\frac{a*b}{p}\right)=\left(\frac{a}{p}\right)*\left(\frac{b}{p}\right)$
• $\left(\frac{a^2}{p}\right)=1,(a,p)=1$

高斯引理(不用记）：p是奇素数，a是整数，（a，p）=1，如果整数a1，a2，…a*（p-1）/2中模p的最小正剩余大于p/2的个数是m，则有$\left(\frac{a}{p}\right)=(-1)^m$ P134

超级重要的二次互反律

p,q是互素的奇素数，则$\left(\frac{p}{q}\right)=(-1)^{\frac{p-1}{2}*\frac{q-1}{2}}\left(\frac{q}{p}\right)$ P137

雅克比符号

勒让德符号的扩展，$\left(\frac{a}{m}\right)=\left(\frac{a}{p_1}\right)...\left(\frac{a}{p_r}\right)$可以（单向）推出无解；P143

雅克比符号性质与勒让德符号一致 P143 二次互反也一样，只是p，q必须是奇数；

一些与雅克比有关的重要式子：也是和勒让德一样，只要限制条件是p不在局限于奇素数，而是奇数 P144

$\left(\frac{1}{m}\right)=1$

$\left(\frac{-1}{m}\right)=(-1)^{\frac{m-1}{2}}$

$\left(\frac{2}{m}\right)=(-1)^{\frac{m^2-1}{8}}$

雅可比和勒让德一些不同的点：

.

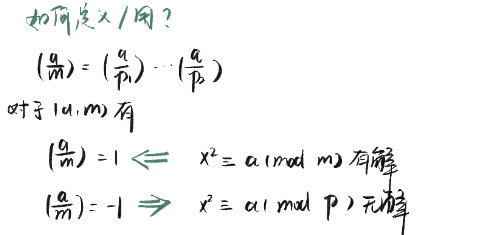
雅可比中上单向的箭头，这里是需要注意一下的

下面放一个大致整理图来的图：