「课程学习」Database-Review

DataBase Review

关系代数

选择： $\sigma_{F}(R)$ SELECT * FROM R WHERE F

投影：$\prod_{A}(R)$ SELECT A FROM R

连接：

笛卡尔积：

现在有两个表如下：

sql> select * from S;
+------+------+
| A    | B    |
+------+------+
|    1 |    2 |
|    3 |    3 |
|    5 |    9 |
+------+------+
3 rows in set (0.00 sec)

sql> select * from R;
+------+------+
| B    | C    |
+------+------+
|    2 |    1 |
|    7 |    2 |
|    3 |    5 |
+------+------+
3 rows in set (0.00 sec)

进行笛卡尔积操作后为：

sql> select * from S,R;
+------+------+------+------+
| A    | B    | B    | C    |
+------+------+------+------+
|    1 |    2 |    2 |    1 |
|    3 |    3 |    2 |    1 |
|    5 |    9 |    2 |    1 |
|    1 |    2 |    7 |    2 |
|    3 |    3 |    7 |    2 |
|    5 |    9 |    7 |    2 |
|    1 |    2 |    3 |    5 |
|    3 |    3 |    3 |    5 |
|    5 |    9 |    3 |    5 |
+------+------+------+------+
9 rows in set (0.00 sec)

笛卡尔积的连接会对两个表的每一列进行排列组合

等值连接

$\theta$ 为“＝” 的连接运算称为等值连接。它是从关系R与S的笛卡尔积中选取A、B属性值相等的那些元组。即等值连接为：

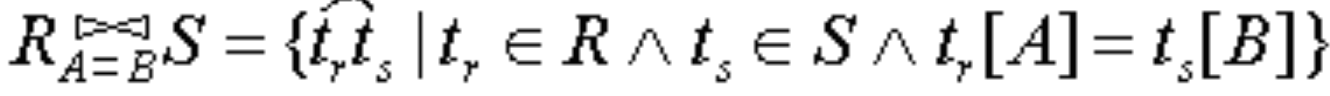
自然连接

自然连接（Natural join）是一种特殊的等值连接，它要求两个关系中进行比较的分量必须是相同的属性组，并且要在结果中把重复的属性去掉。即若R和S具有相同的属性组B，则自然连接可记作：

外连接

左连接

在自然连接的基础上补上左集合中没有的列。没有对应值的项补null

右连接

在自然连接的基础上补上右集合中没有的列。没有对应值的项补null

外连接就是左连接和右连接的组合。

除法

去看： https://www.jianshu.com/p/d80dbaef637e 讲的好啊

还有：https://blog.csdn.net/qq_35361859/article/details/105027905 也不错

---

SQL语句的一些高级操作

WHERE

# between and
select * from my_auto where age between 20 and 22;

# in
select * from my_auto where age in (20,30);

# like or not like
select * from my_auto where age like 'Li%' # 以Li开头的学生
select * from my_auto where age like 'Li_' # 代替任何一个字符

总结

1. where 子句的目的是通过条件匹配进行数据的筛选，数据筛选的原理是在数据表（磁盘）进行；
2. where中可以通过多种运算符来实现数据匹配：比较，逻辑，空运算，匹配运算；
3. 在使用多种运算符的时候，需要考虑运算符的优先级；

DISTINCT

Distinct 去重针对的是所有查出来的字段数据，记录相同则去重，而不是某一个字段值重复；

select distinct * from my_student;

GROUP BY

1. 语法：where 后 gourp by class_name

select class_name from my_student group by class_name

2. Group by 分组原理

• 按照分组字段，将获取到的记录分为几块
• 保留每块的第一条记录

3. group by 的目的： 实现分组统计，分组统计主要要用到一下的聚类函数

• count(*/字段名)： 统计分组字段对应的记录数量
• max(字段名)：统计分组后某个字段的最大值
• min(字段名)：统计分组后某个字段的最小值
• avg(字段名)：统计分组后某个字段的平均值
• sum(字段名)：统计分组后某个字段的和

HAVING 子句

定义：where是从磁盘读取数据时进行判断，而在数据进入内存之后where就不能生效了，HAVING是完全针对进入内存后的数据进行判定。

1. HAVING 语法： HAVING几乎能做所有WHERE能做的事情：HAVING条件判断

select * from my_student having id = 1;	

2. having主要针对group by后的统计结果进行判断

比如: 统计班级人数大于1的班级

select count(*) number,class_name,group_concat(name) from my_student group by class_name having number > 1;

注意： having 子句中用到的字段，必须在select后出现过，即字段从磁盘读入到内存当中。

3. having 条件判断中可以直接使用聚类函数

上面语句也可以替换为：

select count(*) , class_name,group_concat(name) from my_student group by class_name having count(*) > 1;

ORDER BY 子句

定义：order by即通过某个字段，使得表对应的校对集实现升序或者降序排序。

1. order by语法： order by 字段 [ASC][DESC] ; 其中ASC是升序，DESC为降序

select * from my_student order by age;

EXISTS

EXISTS的子查询不反回任何的数据，只会产生逻辑真值 true/flase

语法：

查询所有选修了1号课程的学生姓名

select sname
from Student
where exists(select * from sc,Student where sc.sno = Student.sno);

EXISTS还可以表示关系代数中的除法操作：

比如：查询至少选修了学号为‘200215121’选修的全部课程的学生号码

关系代数为：
$\pi_{sno,cno}(SC) \div \pi_{cno}(\sigma_{'200215121'}(SC))$
SQL语句为：

可以理解为for循环嵌套

SELECT DISTINCT sno
FROM SC SCX
WHERE NOT EXISTS
    (SELECT *
    FROM SC SCY
    WHERE SCY.sno='201215122' AND NOT EXISTS
        (SELECT *
        FROM SC SCZ
        WHERE SCZ.sno=SCX.sno AND SCZ.cno=SCY.cno));

视图

定义视图

1. 语法：

CREATE VIEW <视图名> [<列名>, <列名>, …]

AS <子查询>

[WITH CHECK OPTION]

其中子查询可以是任意的SELECT语句，是否可以含有ORDER BY子句和DISTINCT短语，则取决于具体系统的实现；

2. WITH CHECK OPTION

作用：在对视图进行插入修改和删除时，关系数据库管理系统会自动记上select中的条件；

例如：建立信息系学生的视图，并要求进行修改和插入操作时仍然需要保证该视图有信息系的学生；

CREATE VIEW IS_Student
AS 
SELECT Sno,Sname,Sage 
FROM Student
WHERE Sdept='IS'
WITH CHECK OPTION;

3. 带有聚焦函数的语句

例如： 将学生的学号和平均成绩定义为一个视图；

CREATE VIEW S_G(Sno,Savg)
AS
SELECT Sno,AVG(Grade)
FROM SC
GROUP BY Sno;

删除视图

1. 语法：DROP VIEW [CASCADE]

CASCADE级联删除语句把视图和由他导出的所有视图一起删除了；

查询和更新视图

视图建立完之后就可以对视图像数据库一样进行查询和更新啦。

视图的作用：

1. 视图能够简化用户的操作

2. 视图是用户能以多种角度看待同一数据

3. 视图对重构数据库提供了一定程度的逻辑独立性

4. 视图能够对机密数据提供安全保护

5. 适当利用视图可以更加清晰地对表达查询

数据库的安全性

授权：授予和收回

1. GRANT

GRANT语句的一般格式为：

GRANT <权限>[，<权限>]
ON <对象类型><对象名>[,<对象类型><对象名>]
TO <用户>[,<用户>]
[WITH GRANT OPTION]

• 接受授权的用户可以是一个或者多个具体用户，也可以PUBLIC，即全体用户。
• 如果是所有权限则可以使用ALL PRIVILEGES

如果指定了WITH GRANT OPTION子句，则获得某种权限的用户还可以把这种权限再授权其他的用户。没有的用户则不能传播该权限。

例如：

-- 把查询Student表的权限授权给用户U1
GRANT SELECT ON TABLE Student TO U1;

-- 把对Student和Course表的全部操作权限授予用户U2和U3
GRANT ALL PRIVILEGES ON TABLE Student,Course TO U2,U3;

-- 把对表SC的查询权限授予所有用户并允许将该权限进行传播
GRANT Select ON TABLE SC TO PUBLIC WITH GRANT OPTION;

-- 每个学生具有查询SC表中自己信息的权限
GRANT Select ON SC WHEN USER()=Sname TO PUBLIC;

2. REVOKE

REVOKE 语句的意义是从某个角色/角色组那里收回权限

REVOKE <权限>[，<权限>]
ON <对象类型><对象名>[,<对象类型><对象名>]
FROM <用户>[,<用户>]

视图机制

通过为不同的用户定义不同的视图，把数据对象限制在一定的范围内。也就是说通过视图机制把要保密的数据对无权存取对用户隐藏起来，从而自动对数据提供一定程度的安全保护。

例如：将视图CS_Student的SELECT权限授予U1

GRANT SELECT
ON CS_Student
TO U1;

外键约束

定义：外间FOREIGN KEY，指在一张表中有一个字段指向另一个表的主键字段，并且通过外键关联会有一些约束效果

思考：在学习表关系的时候，在一对多或者多对多的时候，都会在一张表中增加一个字段来指向另一个表的主键，但是此时其实指向没有任何的实际含义，需要人为的去记住，这样有啥意义呢？

引入：如果只是需要人为的去记住对应的关系，没有任何数据库本身去控制的话，那样的存在没有价值。外键就是负责这样的一个作用啦。

外键

定义：外键就是在设定呢字段属于其他表的主键后，使用FOREIGN KEY关键字让表字段与另外表的主键产生内在关联关系。

1. 创建表的使用 FOREIGN KEY (Cno) REFERENCES Course(Cno) 【标准SQL语句】

CREATE TABLE SC
(Sno CHAR(9) NOT NULL,
 Cno CHAR(4) NOT NULL,
 Grade SMALLINT,
 PRIMARY KEY (Sno,Cno),
 FOREIGN KEY(Sno) REFERENCES Student(Sno),
 FOREIGN KEY(Cno) REFERENCES Student(Cno)
);

外键约束

定义：外键约束，即外键的增加之后对应的父表和子表都有相应的约束关系

1. 外键增加后默认字段插入的数据对应的外键字段必须在浮标存在，否则会报错
2. 外键增加后默认父表主键如果在外键值有使用，那么不能更新主键值，也不能删除主键所有记录
3. 外键的作用：

• 限定子表（外键所在表）不能插入主表中不存在的外键值（不能更新）
• 限定父表（主键被引用）不能删除或者更新子表有外键引用的主键信息

4. 可以在创建外键的之后制定外键的约束效果：即控制父表的操作对子表的影响

• 控制情况

  • on update：父表更新与子表有关联的主键时
  • on delete：父表删除与子表有关联的主键时

• 控制效果

  • cascade：级联操作，即父表怎么样，子表有对应关系的记录就怎么样
  • set null：置空操作，即父表变化，子表关联的记录对应的外键字段置空（注意：能够使用的前提是外键对应的字段允许空）
  • restrict/no action：严格模式，即不允许父表操作

• 通常的搭配如下：

  • on update cascade: 父表更新，子表级联更新
  • on delete cascade: 父表删除，子表对应外键置空

总结

1. 外键约束分为父表的约束和对子表的约束，其中子表的约束是固定的不能插入父表不存在的外键值
2. 父表外键约束可以通过设定on update和on delete事件来控制，控制方式有cascade，set null和restrict三种
3. 外键的强大约束作用可以保证数据的完整性和有效性
4. 外键的强大约束有可能操作负面影响：数据维护变的困难，所以实际开发中需要根据需求选择使用
5. 外键总有InnoDB存储引擎支持，Mylsam不支持

用户定义的完整性

定义：用户定义的完整性就是针对某一个具体应用的数据必须满足语义要求。

1. 属性上的约束条件

在创建表时可以给表中的一些字段规定一些属性：

• 列值非空（NOT NULL）
• 列值唯一（UNIQUE）
• 检查列值是否满足一个条件表达式（CHECK 短语）

CREATE TABLE SC
(Sno CHAR(9) NOT NULL,
 Cno CHAR(9) UNIQUE,
 GRADE NUMBER CHECK(GRADE BETWEEN 0 AND 100);

2. 元组上的约束

与属性上的约束条件定义类似，不过元组级的限制可以设置不同属性之间的取值互为约束条件。

语法： CHECK(…)

CREATE TABLE Student
(
	Sno CHAR(9),
  Sname CHAR(8) NOT NULL,
  Ssex CHAR(2),
  Sage SMALLINT,
  Sdept CHAR(20),
  PRIMARY KEY(Sno),
  CHECK(Ssex='女' OR Sname NOT LIKE 'Ms.%')
);

当往表中插入援助否则修改属性的时候，关系数据库关系系统会自动检查元组上的约束条件时候被满足，如果不满足则操作被拒绝执行。

完整性约束命名子句

SQL 在 CREATE TABLE语句中提供了完整性约束命名子句CONSTRAINT，用来对完整性约束条件命名，从而可以灵活地增加、删除一个完整性约束条件。

1. 完整性约束命名子句

语法：CONSTRAINT <完整性约束条件名><完整性约束条件>

CREATE TABLE Student
(
	Sno NUMBERIC(6)
  	CONSTRAINT C1 CHECK(Sno BETWEEN 90000 AND 99999),
  ...
)

2. 修改表中的完整性限制

可以使用ALTER TABLE 语句修改表中的完整性限制

ALTER TABLE Student
	DROP CONSTRAINT C1;

范式

几个函数依赖

设R(U)是属性集U上的关系模式，X，Y是U的子集。若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等，而在Y上的属性值不等，则称X函数确定Y或Y函数依赖于X，记住X->Y

部分函数依赖：

设X,Y是关系R的两个属性集合，存在X→Y，若X’是X的真子集，存在X’→Y，则称Y部分函数依赖于X。

例子：学生基本信息表R中（学号，身份证号，姓名）当然学号属性取值是唯一的，在R关系中，（学号，身份证号）->（姓名），（学号）->（姓名），（身份证号）->（姓名）；所以姓名部分函数依赖于（学号，身份证号）；

完全函数依赖：

设X,Y是关系R的两个属性集合，X’是X的真子集，存在X→Y，但对每一个X’都有X’!→Y，则称Y完全函数依赖于X。

=例子：学生基本信息表R（学号，班级，姓名）假设不同的班级学号有相同的，班级内学号不能相同，在R关系中，（学号，班级）->（姓名），但是（学号）->(姓名)不成立，（班级）->(姓名)不成立，所以姓名完全函数依赖与（学号，班级);

传递函数依赖：

设X,Y,Z是关系R中互不相同的属性集合，存在X→Y(Y !→X),Y→Z，则称Z传递函数依赖于X。

例子：在关系R(学号 ,宿舍, 费用)中，(学号)->(宿舍),宿舍！=学号，(宿舍)->(费用),费用!=宿舍，所以符合传递函数的要求；即费用传递函数依赖于学号

属性集的函数依赖

就是将所有的可以推导出来的函数依赖关系全部给加进去，需要注意的就是有一个和空集的关系

剩下的就是对各个元素闭包的排列组合；比如上面的例题中 (A)$_+$ = ABC, 所以他就对应了如图的ABC的所有排列组合情况再加一个对空集对关系。

码

候选码的概念

这样一个集合，他可以推出所有的属性，但是他的任意一个真子集无法退出所有的属性。

.

如何求候选码？

1. 只出现在左边的一定是候选码中的元素
2. 只出现在右边的一定不是候选码中的元素
3. 左右都出现的不一定
4. 左右都不出现的一定是候选码中的元素

在确定了可能出现的元素之后就可以使用闭包运算进行测试：如果组合可以推出所有的属性话就说明是候选码。

,

如果三个一组推不出来的话，就再加变成4个一组

闭包：BD的闭包 是指由BD能推出来的所有属性

主属性： 候选码中的属性都是主属性

第一范式

定义：第一范式，在设计表存储数据的时候，如果表中设计的字段存储的数据，在取出来使用之前还需要额外的处理（拆分）就不符合1NF，第一范式就是处理数据颗粒度大的问题

1.案例:设计一张学生选修课成绩表

学生	性别	课程	教室	成绩	学习时间
张三	男	PHP	101	100	2月1日,2月28日
李四	女	Java	102	90	3月1日,3月31日
张三	男	Java	102	95	3月1日,3月31日

2.以上表设计是一种非常常见的数据,但是如果想要知道学生上课的开始时间和结束时间,那就意味着这个学习时间取出之后需要再进行拆分,因此就不符合1NF。要保证数据取出来就可以直接使用,就需要将学习时间进行拆分。

学生	性别	课程	教室	成绩	开始时间	结束时间
张三	男	PHP	101	100	2月1日	2月28日
李四	女	Java	102	90	3月1日	3月31日
张三	男	Java	102	95	3月1日	3月31日

总结：

1. 要满足1NF就是要保证数据在实际使用的时候不用对字段数据进行二次拆分
2. 1DF的核心就行数据要有原子性（不可拆分）

第二范式

以上数据表的设计中满足了原子性，但是学生在某个课程中应该只有一个考试成绩，也就是说学生对应的课程的成绩应该是有唯一性的，那么以上数据表应该如何进行设计呢？

引入：要解决以上问题，其实很简单就是学生姓名和课程名字应该说唯一的，那么只要增加一个复合主键即可。

定义： 第二范式（2NF），在数据表的设计过程中如果有复合主键（多字段主键），且表中有字段且并不是由整个主键来确定，而是依赖主键中的某个字段（主键的部分）：存在字段依赖主键的部分的问题，称之为部分依赖：第二范式就是要解决表设计中非主属性对主属性的部分依赖。

1. 以上表中性别有学生决定，而不受到课程影响；同时教室由课程决定，而不受到学生影响。此时形成了字段部分依赖部分主键的情况，因此会存在部分依赖问题，也就不满足第二范式。
2. 解决方案：就是让字段不会存储依赖部分主键的问题，因此需要做的就是增加一个逻辑主键字段：性别依赖学生但学生不是主键，教室依赖课程也不是主键。

3. 以上虽然解决了依赖问题，但是学生和课程又不具有唯一性了，所以应该增加符合唯一键：unique(学生，课程)

总结：

1. 第二范式就是解决字段部分依赖主键的问题，也就是部分字段依赖的问题

思考： 上述表虽然满足了1NF和2NF，但是总感觉怪怪的，理论上讲性别逻辑主键除外，实际业务主键还是学生和课程，这个表应该是学生与课程对应的成绩，为什么会出现性别和教室呢？

引入：之所以会出现上述矛盾，原因就是我们将数据都揉到了一张表里面，而且出现了性别依赖学生，而学生依赖ID，形成了字段性别依赖非主键字段学分的问题，也就是触法了3NF的问题。

第三范式

定义：第三范式（3NF），理论上讲，应该一张表中的所有字段都应该直接依赖主键（逻辑主键：代表的是业务主键），如果表设计中存在这样一个字段，并不直接依赖主键，而是通过某一个非主键字段依赖，最终实现依赖主键：把这种不是直接依赖主键，而是依赖主键非主键字段的依赖关系称之为传递依赖。第三范式就是要解决传递的问题。

1. 第三范式的解决方案：如果某一个表中有字段依赖非主键字段，而被依赖字段依赖主键，我们就应该将这种非主键依赖关系进行分离，单独形成一张表。

学生表：

课程表：

2. 此时，虽然性别依然依赖姓名而不是Stu_id, 教室依赖课程而不是Class_id, 那是因为Stu_id和Class_id代表逻辑主键，而不是实际的业务主键，学生表的实际主键应该是姓名，课程表的实际主键应该是课程
3. 新学生选修课成绩表的设计，应该就是去的对应学生表和课程表的ID

总结

1. 第三范式是不允许传递依赖：即有字段依赖非主键字段；
2. 消除传递依赖的方案就是将相关数据对应创建一张表；

第三范式的模式分解

求出第三范式对应函数集的最小函数依赖 Fm，使用左部相同合并原则：

Fm中左边相同的合并成一个数据表

例1：U=(A,B,C,D,E,G) F={BG->C，BD->E，DG->C，ADG->BC，AG->B，B->D} 若R不是3NF，将R分解为无损且保持函数依赖的3NF。

很简单可以求出候选键为AG

1. 求最小函数依赖

$(BG)^+$ = {BCDEG} G在其中，删除

$(BD)^+$ = {BD} , E不在其中，保留

$(DG)^+$ = {DG}, C不在其中，保留

$(ADG)^+$ = {ABCDG}, B在其中，C也在其中，删除

$(AG)^+$ = {AG}, B不在其中，保留

$(B)^+$ = {B} , D不在其中保留

可以得到：F = {BD->E, DG->C, AG->B, B->D}

接下来判断一下左边有没有冗余；

BD->E: $(B^+)$=BD, D 在里面，所以D有冗余

$(D^+)=D$, B不在里面所以B没有冗余

所以用B->E 替换，BD->E

同理可以得到Fm = {B->E, DG->C, AG->B, B->D}

2. 根据左部相同原则进行合并

根据左部相同原则可以得到：

R1 = BED, R2 = CDG, R3 = ABG

.

因为AG已经在R3中了所以得到的分解是无损分解

BCNF范式

在3NF的基础上如果所有的函数依赖的左边都是超码，那这个关系就满足第三范式；如果有一个不是超码就不满足；

超码： 一个码的闭包如果就是这个集合，那这个码就叫做超码

BCNF范式的模式分解

…

Armstrong 公理系统

设U为属性集总体，F是U上的一组函数依赖，于是又关系模式R<U,F>，对于R<U,F>来说有以下的推理规则

由上面的三个公理我们可以得到：

最小函数依赖集

F中的每一个依赖，都不可以被其他的依赖推出，且右边一定是单元素

如何求最小依赖集？

Step1： 把右边的元素拆分成单个的

Step2： 对所有的依赖意义排查，找出多余的

.

排查A->B： 把A->B去掉,那么F=(B->A, B->C,A->C, C->A) 且(A)_+ = AC,不包含B,所以排除嫌疑,保留

排查B->A：把B->A去掉,那么F={A->B,A->C,C->A} 且(B)_+=BCA,包含A,就是嫌疑人,剔除

…

注：由于排查的顺序不一样可能会造成最小依赖集的不同

模式分解

无损分解

分解之后可以自然连接结合起来

.

保持函数依赖

保持函数依赖就是F分解之后还能够还原回来

考题：如何把数据库分解成3NF，并保持无损分解和函数依赖

Step1： 求出最小函数依赖集

Step2：把不在F中的属性全部找出来，单独分出一类，并从这些属性中删除

Step3：把每个依赖左边相同的分成一类

Step4：如果候选码没有出现在分类中，把任意一个候选码作为一类

.

例：U=(A,B,C,D,E) F={AB->C，C->B，D->E，D->C} 若R不是3NF，将R分解为无损且保持函数依赖的3NF。

解：易求得，码是AD，属于1NF

1. 第一步：U1=ABC U2=BC U3=DCE

2. 第二步：

   将R分解为ρ={
   R1({A,B,C}，{AB->C})，
   R2({B,C}，{C->B})，
   R3({D,E}，{D->E,D->C}) }

   合并吸收：
   ρ={ R1({A,B,C}，{AB->C,C->B})，
   R2({D,E}，{D->E,D->C}) }

3. 第三步：不是无损连接，添加码。

   R3({A,D}，{∅})

   所以ρ={ R1({A,B,C}，{AB->C,C->B})，
   R2({D,E}，{D->E,D->C}),
   R3({A,D}，{∅}) }

数据库设计

ER图转关系模式

去看： https://blog.csdn.net/Flora_SM/article/details/84645752 这里讲的非常好！

高阶操作总结

自身连接查询

对自身进行笛卡尔积连接

例如：选修关系elective(sno, cno, grade)

• 查询选修了CO2和CO4课程的学生的学号

SELECT e1.sno from elective e1,elective e2 WHERE e1.sno = e2.sno AND e1.sno='CO2' AND e2.sno='CO4'

EXIST实现除法操作

除法的语义

除法的真正的语义应该为包含。常见的表述形式有：

• 查询至少…的对象
• 查询xx了全部的对象
• 查询xx包含了xx的对象、

举个栗子

假设教学数据库中已建立三个关系：

学生关系 student(sno, sname, sex, birth, height, class, address)

课程关系course(cno, cname, credit)

选修关系elective(sno, cno, grade)

检索学习全部课程的学生姓名。

SELECT s.sname 
FROM student s
WHERE NOT EXIST(
	SELECT * 
  FROM course c
  WHERE NOT EXIST(
  	SELECT * 
    FROM elective e
    WHERE 
    e.sno=s.sno AND c.cno=e.cno
  )
);

检索至少选修了课程号为S08的学生的学号

关系代数： $\pi_{\text {sno,cno }}( elective ) \div \pi_{\text {cno }}(\sigma_{cno='s08'}( (elective))))$

SQL语句：

SELECT DISTINCT e1.sno 
FROM elective e1
WHERE NOT EXIST(
	SELECT *
  FROM elective e2
  WHERE 
  e2.cno='s08' AND NOT EXIST(
  	SELECT * 
    FROM elective e3
    WHERE
    e1.sno=e3.sno AND e2.cno=e3.cno
  )
)

那些常用的关键词

• REFERENCES
• FOREIGN
• GRANT
• ALL PRIVILEGES
• PRIMARY KEY
• DESC【降序】
• CASCADE